To determine initial control loop tuning values, we must first look at what type of process we are dealing with and understand what the primary tuning constants P (proportional gain) and I (integral time) do. Processes can be classified as accumulating or non-accumulating.
- Accumulating – Processes where material or energy are accumulated or held. Levels are accumulating because they hold volume or mass. Vapor pressures can be accumulating as they accumulate gas. Some temperatures are accumulating because they hold heat capacity.
- Non-accumulating – Flows, hydraulic pressures, and temperature due to combustion.
Why is this important? Integral time is based on the time it takes a process to accumulate (see the figure). For example, if it takes about 5 minutes to fill a tank halfway at full feed, the integral time will be somewhere in the neighborhood of 5 minutes. Conversely, the time it takes for a change in valve position to reach the flowmeter is a matter of seconds. This would be a good start for the integral time for the flow.
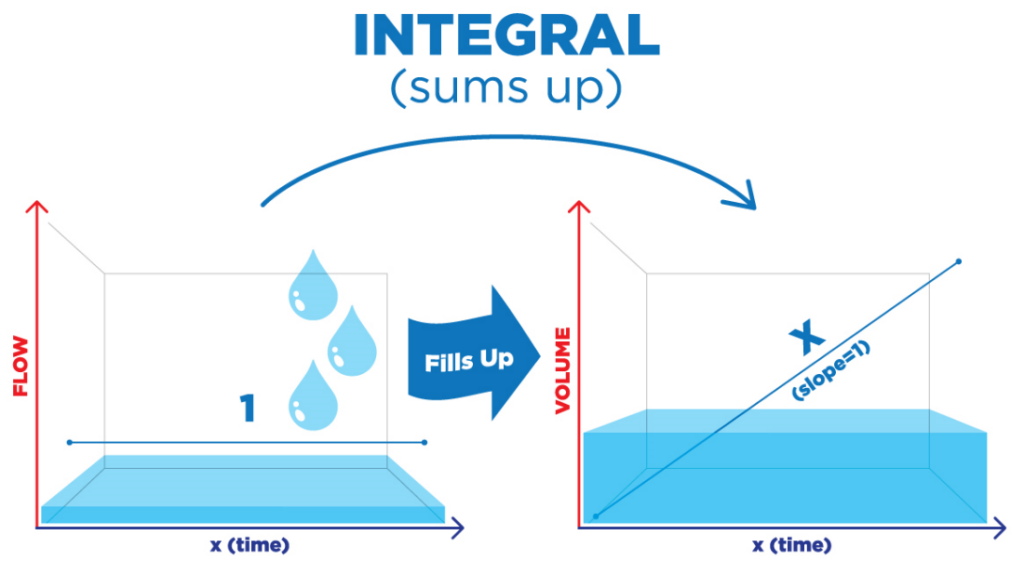
Let’s look at this general rule at play. The integral time (in time per repeat) is relative to the accumulation time. A large time to accumulate means a large integral time; conversely, a short accumulation time means a small integral time. Once we get an integral starting point, we can work on proportional gain.
Proportional gain is relative to size. For example, a large tank could have a very large proportional gain and stay in control. That might mean, for instance, a value of 20 for a very large vessel, where a small tank could only tolerate a smaller proportional, say 2. When dealing with proportion, keep in mind how far we want the valve to travel based on the error (difference between setpoint and measurement). Since we don’t want the tank to run empty or overflow and the integral time is rather long, we would want the proportional to be a value of 1 or greater.
Since the process for a flow is small compared to a level, we would expect our proportional gain to be small, most likely less than 1. Pressures can be small if we are trying to control the hydraulic pressure in a line, or large if we are controlling the vapor pressure of a large vessel. Typically, larger processes are accumulating while smaller ones are non-accumulating. So process size and proportional are relative.
Derivative is something we want to avoid unless we have a process with excursions, such as a reactor temperature that has a rapid rise and fall due to reactivity. In this instance, we are looking at the rate of change and trying to mirror that with the derivative time.
These few simple rules can help get a control loop into a position where we can fine tune it to get the kind of recovery curve desired from process upsets. Keeping in mind that integral time is relative to accumulation and proportional is relative to size will help get the loop tuning process started.
For a facility to run well, the people and the automation systems must work together seamlessly and safely. Learn How to Evaluate and Mitigate Process Control Safety Risks.
Rocky Chambers (rocky.chambers@rockwellautomation.com) is an automation and control systems specialist at Rockwell Automation. With more than 45 years of experience in a variety of industries, he serves on the ISA106 committee and specializes in state-based control, fired equipment, and safety instrumented system (SIS) implementation.

